APIO 2013 - Taskauthor

Part 1 - shortest-path algorithms

In this subproblem, we're asked to create test cases that break certain shortest-path algorithms through TLE.

This is very educational because it forces you to analyze the bottlenecks of these algorithms and how exactly they work.

Subtasks 1 and 3 - breaking Floyd-Warshall

The Floyd-Warshall algorithm always uses exactly $V^3$ iterations.

This means we can simply set $V$ to 101 and $E$ to 0 to force TLE.

Code

Copy
print(101)  # Generate the graph
for i in range(101):
	print(0)

print(1)  # Single query
print(0, 1)

Subtasks 2 and 5 - breaking Bellman-Ford

The Bellman-Ford algorithm normally uses exactly $E(V - 1)$ iterations, but in this case, it's slightly optimized.

However, we can still force the algorithm to use exactly $E(V - 1)$ iterations.

Firstly, note that we must have $E \geq V$ or else the algorithm will break early.

If we look at the implementation of this specific Bellman-Ford algorithm, note that we "relax" edges connected to node 1, then node 2, etc.

This means that if we have a straight line from node $V - 1$ to node 0 (and no other edges), then only 1 edge will be relaxed per loop!

We can also add some self-edges (with positive weights) from node 0 to itself to increase $E$ without triggering an early break, since it's never optimal to go from a node to itself via a self-edge.

$(V, E) = (100, 1100)$ for subtask 2 and $(V, E) = (300, 347)$ for subtask 5 let us force TLE.

Code

Copy
print(300)  # Change (300, 48) to (100, 1011) for subtask 2
print(48, end=" ")
for i in range(48):
	print(0, 1, end=" ")  # Self edges
print()
for i in range(1, 300):
	print(1, i - 1, 1)

print(10)  # 10 queries
for i in range(10):
	print(299, 0)

Subtasks 4 and 6 - breaking Dijkstra

At first glance, these subtasks seem impossible - Dijkstra's algorithm always has a complexity of $\mathcal{O}(E \log V)$!

... or does it?

Note that the $\mathcal{O}(E \log V)$ complexity is only true if there are no negative edges.

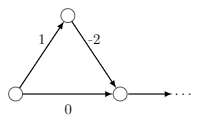
What happens when we have negative edges in the graph? Consider the following construction:

If there were no negative edges, then we'd only iterate through the edges connected to the rightmost node once.

However, notice how in the above construction, we will iterate through those edges twice.

This means that if we chain $N$ of those triangles together, then Dijkstra's algorithm will use $2^N$ iterations - far more than the expected $V \log E$!

Using 16 triangles, we are able to force TLE.

Code

Copy
print(33)
print(0)
print(1, 0, 1)
print(1, 1, 1)
for i in range(2, 31, 2):
	print(1, i, -2 * (2 ** (i // 2)))
	print(2, i + 1, 2 ** (i // 2), i, 0)

print(7)
for i in range(7):
	print(32, 0)

Part 2 - the "mystery" problem

Subtask 7 - forcing TLE

Code

Copy
print(250, 1501)
for i in range(300):
	for j in range(i + 1, 250, i + 1):
		print(i, j)
for i in range(88):
	print(1, 2 * i + 3)

Subtask 8 - forcing not TLE

Code

Copy
print(753, 1501)
for i in range(1, 752):
	if i != 1:
		print(0, i)
	print(i, 752)

Copy
int main() {
	FOR(TC, 1, 7) {
		setOut("apio-2013-taskauthor_" + ts(TC) + ".out");
		int V;
		vpi adj[300];
		vpi query;
		if (TC == 1 || TC == 3) {
			V = 101;
			query.pb({0, 0});
		} else if (TC == 2) {