Eulerian Tours

Resources

Explanation

First, let's define what an Eulerian path is.

An Eulerian path is a path that goes through every edge once.

Similarly, an Eulerian cycle is an Eulerian path that starts and ends with the same node.

An important condition is that a graph can have an Eulerian cycle (not path!) if and only if every node has an even degree.

Now, to find the Eulerian cycle we run a modified DFS. The DFS goes through only unvisited edges and the same edge can be processed multiple times throughout the DFS, so we remove it from the graph at the first visit.

The algorithm described is Hierholzer's Algorithm.

Implementation

Time Complexity: $\mathcal{O}(E)$

Copy
#include <bits/stdc++.h>
using namespace std;

int n, m;
vector<vector<pair<int, int>>> g;
vector<int> path;
vector<bool> seen;

void dfs(int node) {
	while (!g[node].empty()) {

Copy
path = []


def dfs(node: int):
	stack = [node]
	while stack:
		u = stack[-1]
		if g[u]:
			son, idx = g[u].pop()
			if not seen[idx]:

Explanation

The condition of existence for an eulerian path in a directed graph is: At most one node has $out_i - in_i=1$ and at most one node has $in_i - out_i=1$. This property is because an Eulerian path or cycle leaves a node the same number of times it enters the node. In a directed graph the exception are the start node and the end node.

Implementation

Time Complexity: $\mathcal{O}(E)$

Copy
#include <bits/stdc++.h>
using namespace std;

int n, m;
vector<vector<int>> g;
vector<int> in, out, path;

void dfs(int node) {
	while (!g[node].empty()) {
		int son = g[node].back();

Copy
path = []


def dfs(start: int):
	stack = [start]
	while stack:
		node = stack[-1]
		if g[node]:
			son = g[node].pop()
			stack.append(son)

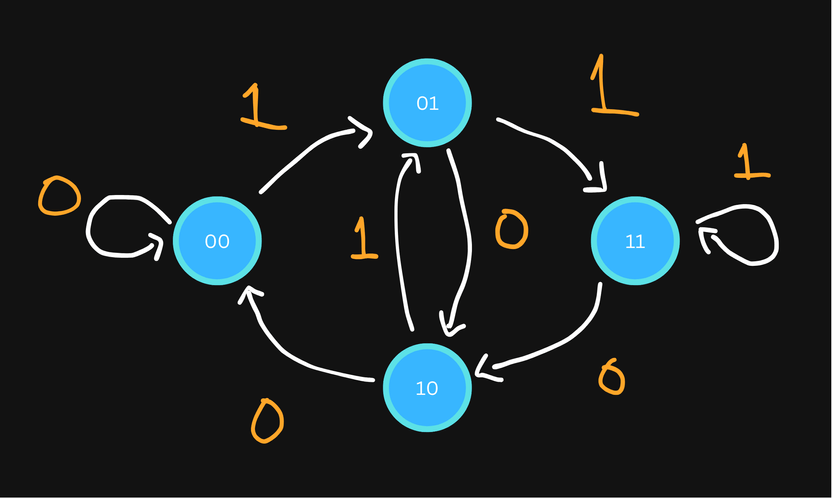
De Bruijn Sequences

A De Bruijn sequence is a string of minimum length that contains every string of length $n$ exactly once as a substring, for a fixed alphabet with $k$ letters. In our case $k=2$ because we only have $0$ and $1$.

Let's take a look at some particular cases:

1. $n=2$ $\rightarrow$ 00110
2. $n=3$ $\rightarrow$ 0001011100

We can visualize the transitions - adding $0$ or $1$ - using an oriented graph whose nodes contain a string of length $n-1$.

An Eulerian path in the above graph represents a valid solution. The starting node has $n-1$ characters and there are $k^n$ edges that each add one more character, so the length of a De-Bruijn string is $k^n+n-1$.

Implementation

Time Complexity: $\mathcal{O}(2^N)$

Copy
#include <bits/stdc++.h>
using namespace std;

int main() {
	int n;
	cin >> n;
	if (n == 1) {
		cout << "10" << endl;
		return 0;
	}

Copy
n = int(input())

if n == 1:
	print("10")
	exit()

adj = [[] for _ in range(1 << (n - 1))]

for node in range(1 << (n - 1)):
	son = (node << 1) % (1 << (n - 1))

Problems