| Resources | |||||
|---|---|---|---|---|---|
| CPC | String Matching, KMP, Tries | ||||
| CP2 | |||||
Single String
A Note on Notation:
For a string :
- denotes the size of string
- denotes the character at index starting from
- denotes the substring beginning at index and ending at index
- is equivalent to , represents the prefix ending at
- is equivalent to , represents the suffix beginning of .
- denotes concactinating to the end of . Note that this implies that addition is non-commutative.
Knuth-Morris-Pratt Algorithm
| Resources | |||||
|---|---|---|---|---|---|
| cp-algo | |||||
| PAPS | |||||
| GFG | |||||
| TC | |||||
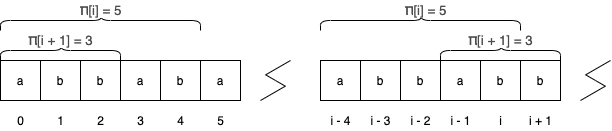
Define an array of size such that is equal to the length of the longest nontrivial suffix of the prefix ending at position that coincides with a prefix of the entire string. Formally,
In other words, for a given index , we would like to compute the length of the longest substring that ends at , such that this string also happens to be a prefix of the entire string. One such string that satisfies this criteria is the prefix ending at ; we will be disregarding this solution for obvious reasons.
For instance, for , , and the prefix function of is . In the second example, because the prefix of length ( is equivalent to the substring of length that ends at index . In the same way, because the prefix of length () is equal to the substring of length that ends at index . For both of these samples, there is no longer substring that satisfies these criteria.
The purpose of the KMP algorithm is to efficiently compute the array in linear time. Suppose we have already computed the array for indices , and need to compute the value for index .
Firstly, note that between and , can be at most one greater. This occurs when .
In the example above, , meaning that the suffix of length is equivalent to a prefix of length of the entire string. It follows that if the character at position of the string is equal to the character at position , then the match is simply extended by a single character. Thus, .
In the general case, however, this is not necessarily true. That is to say, . Thus, we need to find the largest index such that the prefix property holds (ie ). For such a length , we repeat the procedure in the first example by comparing characters at indices and : if the two are equal, then we can conclude our search and assign , and otherwise, we find the next smallest and repeat. Indeed, notice that the first example is simply the case where begins as .
In the second example above, we let .
The only thing that remains is to be able to efficiently find all the that we might possibly need. To recap, if the position we're currently at is , to handle transitions we need to find the largest index that satisfies the prefix property . Since , this value is simply , a value that has already been computed. All that remains is to handle the case where . If , , otherwise .
C++
vector<int> pi(const string &s) {int n = (int)s.size();vector<int> pi_s(n);for (int i = 1, j = 0; i < n; i++) {while (j > 0 && s[j] != s[i]) { j = pi_s[j - 1]; }if (s[i] == s[j]) { j++; }pi_s[i] = j;}return pi_s;}
Python
from typing import Listdef pi(s: str) -> List[int]:n = len(s)pi_s = [0] * nj = 0for i in range(1, n):while j > 0 and s[j] != s[i]:j = pi_s[j - 1]if s[i] == s[j]:j += 1pi_s[i] = jreturn pi_s
Claim: The KMP algorithm runs in for computing the array on a string of length .
Proof: Note that doesn't actually change through multiple iterations. This is because on iteration , we assign . However, in the previous iteration, we assign to be . Furthermore, note that is always non-negative. In each iteration of , is only increased by at most in the if statement. Since remains non-negative and is only increased a constant amount per iteration, it follows that can only decrease by at most times through all iterations of . Since the inner loop is completely governed by , the overall complexity amortizes to .
Problems
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| CSES | Very Easy | Show TagsKMP, Z | ||||
| POI | Easy | Show TagsKMP, Strings | ||||
| Baltic OI | Normal | Show TagsKMP, Strings | ||||
| Old Gold | Hard | Show TagsKMP, Strings | ||||
| POI | Hard | Show TagsKMP, Strings | ||||
| CEOI | Hard | Show TagsKMP | ||||
| POI | Very Hard | Show TagsKMP | ||||
| POI | Very Hard | Show TagsKMP | ||||
Z Algorithm
Focus Problem – try your best to solve this problem before continuing!
| Resources | |||||
|---|---|---|---|---|---|
| cp-algo | |||||
| CPH | |||||
| CF | |||||
Explanation
The Z-algorithm is very similar to KMP, but it uses a different function than and it has an interesting different application than string matching.
Instead of using , it uses the z-function. Given a position, this function gives the length of the longest string that's both the prefix of and of the suffix of starting at the given position.
Here's some examples of what this function might look like:
aabxaayaabaabxaabxcaabxaabxay
Let's also take a closer look at (0-indexed) for the second string. The value for this position is because that's the longest common prefix between the string itself aabxaabxcaabxaabxay and the suffix starting at position aabxaabxay (also 0-indexed).
To efficiently compute this array, we maintain the interval such that is also a prefix, i.e. .
Say we have a position anywhere in . We would then have these two cases:
- If , we know that .
- Otherwise, , meaning that the answer can expand beyond . Thus, we compare character by character from there on.
Implementation
Time Complexity:
C++
#include <algorithm>#include <iostream>#include <string>#include <vector>using namespace std;vector<int> z_function(const string &s) {vector<int> z(s.size());z[0] = s.size();
Python
from typing import Listdef z_function(s: str) -> List[int]:n = len(s)z = [0] * nz[0] = nl, r = 0, 0for i in range(1, n):z[i] = max(0, min(z[i - l], r - i + 1))
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| YS | Very Easy | Show TagsZ | ||||
| CSES | Very Easy | Show TagsKMP, Z | ||||
| CF | Normal | Show TagsDP, Strings | ||||
| CF | Normal | Show TagsZ | ||||
| CF | Hard | |||||
Palindromes
Manacher
Focus Problem – try your best to solve this problem before continuing!
| Resources | |||||
|---|---|---|---|---|---|
| HR | |||||
| Medium | |||||
| cp-algo | |||||
Manacher's Algorithm functions similarly to the Z-Algorithm. It determines the longest palindrome centered at each character.
Let's denote as the maximum diameter of a palindrome centered at . Manacher's algorithm makes use of the previously determined , where incalculating . The main idea is that for a palindrome centered at with the borders and the () values are - probably - mirrors of the () values on the left side of the palindrome. Probably because for some the maximum palindrome might cross the right border. This way the algorithm only considers the palindrome centers that could lead to the expansion of the maximum palindrome.
Time complexity:
C++
#include <bits/stdc++.h>using namespace std;string menacher(string s) {// Preprocess the input so it can handle even length palindromesstring arr;for (int i = 0; i < s.size(); i++) {arr.push_back('#');arr.push_back(s[i]);}
Don't Forget!
If s[l, r] is a palindrome, then s[l+1, r-1] is as well.
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| CF | Normal | Show TagsStrings | ||||
| CF | Normal | Show TagsStrings | ||||
| CF | Hard | Show TagsPrefix Sums, Strings | ||||
Palindromic Tree
A Palindromic Tree is a tree-like data structure that behaves similarly to KMP. Unlike KMP, in which the only empty state is , the Palindromic Tree has two empty states: length , and length . This is because appending a character to a palindrome increases the length by , meaning a single character palindrome must have been created from a palindrome of length
| Resources | |||||
|---|---|---|---|---|---|
| CF | |||||
| adilet.org | |||||
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| APIO | Easy | |||||
| CF | Hard | Show TagsPrefix Sums, Strings | ||||
| MMCC | Very Hard | |||||
Multiple Strings
Tries
Focus Problem – try your best to solve this problem before continuing!
| Resources | |||||
|---|---|---|---|---|---|
| CPH | |||||
| CF | |||||
| PAPS | |||||
A trie is a tree-like data structure that stores strings. Each node is a string, and each edge is a character.
The root is the empty string, and every node is represented by the characters along the path from the root to that node. This means that every prefix of a string is an ancestor of that string's node.
C++
#include <bits/stdc++.h>using namespace std;const int NMAX = 5e3;const int WMAX = 1e6;const int MOD = 1e9 + 7;int trie[WMAX][26];int node_count;bool stop[WMAX];
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| COCI | Very Easy | Show TagsDFS, Strings, Trie | ||||
| IOI | Very Easy | Show TagsDFS, Strings, Trie | ||||
| YS | Easy | Show TagsGreedy, Trie | ||||
| CF | Normal | Show TagsMST, Trie | ||||
| Gold | Normal | Show TagsStrings, Trie | ||||
| CF | Normal | Show TagsStrings, Trie | ||||
| COCI | Normal | Show TagsTrie | ||||
| AC | Normal | |||||
| CF | Normal | Show TagsSmall to Large, Tree, Trie | ||||
| CF | Normal | Show TagsBitmasks, Tree, Trie | ||||
| IZhO | Hard | Show TagsGreedy, Trie | ||||
| JOI | Hard | Show TagsBIT, Trie | ||||
| CF | Hard | Show TagsTree, Trie | ||||
Aho-Corasick
Focus Problem – try your best to solve this problem before continuing!
| Resources | |||||
|---|---|---|---|---|---|
| cp-algo | |||||
| CF | |||||
| GFG | |||||
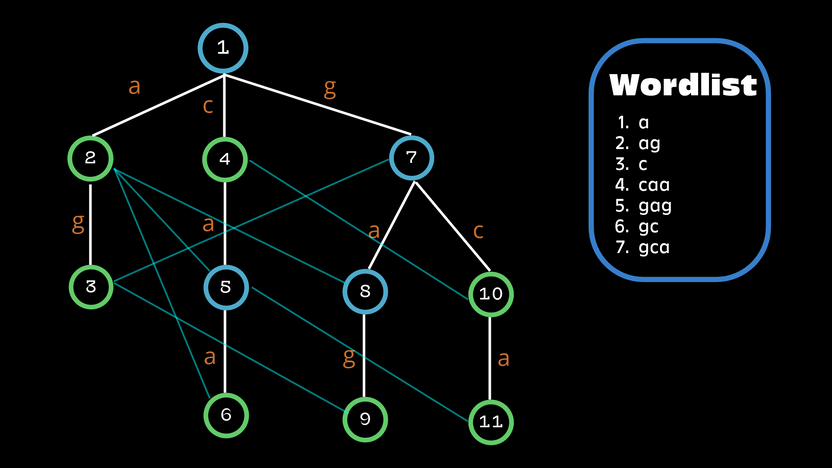
The Aho-Corasick algorithm stores the pattern words in a trie structure, described above. It uses the trie to transition from a state to anoother. Similar to KMP algorithm, we want to reuse the information we have already processed.
A suffix link or failure link for a node is a special edge that points to the longest proper suffix of the string corresponding to node . The suffix links for the root and all its immediate children point to the root node. For all other nodes with parent and letter on the edge the suffix link can be computed by following 's failure link and transitioning to letter from there.
While processing the string the algorithm maintains the current node in the trie such that word formed in the node is equal to the longest suffix ending in .
For example, when transitioning from to in there only are two choices:
- If does have an outgoing edge with letter , then move down the edge.
- Otherwise, follow the failure link of and transition to letter from there.
The image below depicts how the structure looks like for the words .
There is a special case when some words are substring of other words in the wordlist. This could lead to some problems depending on the implementation. Dictionary links can solve this problem. They act like suffix links that point to the first suffix that is also a word in the wordlist. The code below constructs the structure using a BFS.
Time Complexity: - where is the size of the alphabet and the size of the alphabet
C++
#include <bits/stdc++.h>using namespace std;const int MAX_N = 6e5;const int SIGMA = 26;int n;string s;// The number of nodes in trie
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| CF | Easy | Show TagsStrings | ||||
| Gold | Normal | Show TagsStrings | ||||
| CF | Normal | Show TagsStrings | ||||
Problems
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| CSES | Normal | |||||
| CSES | Normal | |||||
| CSES | Normal | |||||
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!