Minimum Cost Flow
Authors: Siyong Huang, Benjamin Qi
Triangle Inequality, Johnson's Algorithm, and Min Cost Flow
Prerequisites
In this section I will briefly walk over my understanding of min cost flow. I would highly recommend reading through CP-Algorithm's Min Cost Flow to understand the solution idea first. Additionally, check the TopCoder tutorial for a more detailed explanation.
Triangle Inequality
In graph theory, the Triangle Inequality states that if there is an edge with weight , and be the shortest path to node (for some reasonable definition of shortest path), then .
| Resources | |||||
|---|---|---|---|---|---|
| Wikipedia | Mainly in geometry, but it has the gist of the idea. | ||||
Johnson's Algorithm
The main idea of Johnson's Algorithm is that if all edge weights are positive, then running Dijkstra's from each node would result in a algorithm. If there are any negative edges, Johnson's Algorithm defines a potential function , such that for every edge , the following holds: . Then, each edge weight can be transformed into , resulting in positive weight. This condition coincides with the Triangle Inequality, so we can arbitrarily pick a node and run a shortest path algorithm to determine this function.
| Resources | |||||
|---|---|---|---|---|---|
| GFG | |||||
| Wikipedia | |||||
Minimum Cost Flow
The general idea of Min Cost Flow is to repeatedly push flow along the shortest path. Since flow graphs have negative edges, each step naively would take time. To speed it up, we can use the same potential function from Johnson's Algorithm to employ Dijkstra for this process. In this case we must use distance from , the source node, as the function. At each step, run Dijkstra's using the function, update the function to match the current distances, and then push flow along the shortest path, reversing edges as needed. Once flow is met or the sink is unreachable, terminate.
Important Clarification
Note that the function stores values before the edge reverses happen. Luckily the triangle inequality's equality case is along the shortest path, meaning that in a flow network it holds both forwards and backwards along edges in the shortest path. This means that although the function does not store the shortest paths, it still satisfies the triangle inequality for all edges.
| Resources | |||||
|---|---|---|---|---|---|
| CP-Algorithms | Note: Does not use optimal solution, but explains the concept well. | ||||
| TopCoder | |||||
Implementation
With all this being said, here is my implementation.
template <int MN, int MM>struct MCF // MN = nodes, MM = edges [assume edges one-directional]{public:int N, M, S, T;int flow[MM * 2], cap[MM * 2], hd[MN], nx[MM * 2], to[MM * 2], cost[MM * 2];int pi[MN], p[MN], d[MN];int vis[MN];void init(int n, int s, int t) {N = n, S = s, T = t;
Also check out Benq's Implementation and KACTL's Implementation (which are a lot better than mine).
Problems
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| CF | Normal | Show TagsMCF | ||||
| CF | Normal | Show TagsMCF | ||||
| CF | Normal | |||||
| CF | Hard | Show TagsBitmasks, MCF | ||||
| CF | Very Hard | |||||
| CF | Very Hard | |||||
Applications
Assignment Problem
Focus Problem – try your best to solve this problem before continuing!
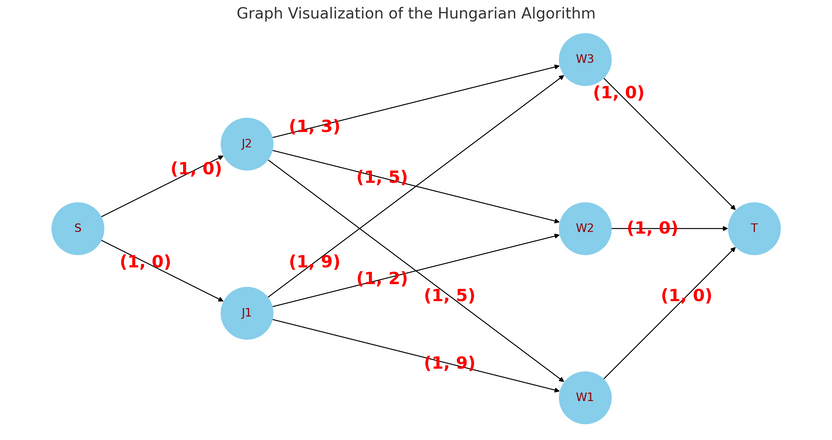
The assignment problem is best understood as a min cost max flow problem. In our formulation, we will assign workers to jobs, , and the cost of assigning the th job to the th worker is .
We will create a flow network with a source node , job nodes , worker nodes , and a sink node .
We will have the following edges:
- with
- with
- with
The answer will be the minimum cost of the max flow of the graph. An example:
To solve this, we will use the min cost max flow algorithm detailed above. In every iteration of the algorithm, we will assign a job to a worker. In each iteration, we will first assign the job to an auxiliary worker, then we will try to find an augmenting path with minimum cost. To optimize this, we will only run Dijkstra on the worker nodes. For details, refer to the code.
Since there are iterations (for each job) and each iteration takes time, the overall time complexity is .
Implementation
From Wikipedia (which is then copied from e-maxx):
#include <bits/stdc++.h>using namespace std;int ckmin(int &a, int b) { return a > b ? ((a = b), true) : false; }/*** @return the jobs of each worker in the optimal assignment,* or -1 if the worker is not assigned*/template <class T> vector<int> hungarian(const vector<vector<T>> &C) {
| Resources | |||||
|---|---|---|---|---|---|
| Wikipedia | |||||
| YouTube - Algorithms Thread | |||||
| Topcoder | |||||
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| CF | Easy | |||||
| Kattis | Easy | |||||
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!