Often, when running operations or dynamic programming on trees, we only need to keep track of a few key nodes and their relationships. If we are able to isolate the few relevant nodes that keep the structure of the tree intact, while still maintaining the relationships between key nodes, we can cut our time complexity down significantly.
Example - Leaf Color
Focus Problem – try your best to solve this problem before continuing!
Naive Solution
We can sum the number of vertex sets that satisfy the condition with degree vertices having color across all to obtain an answer.
We define to be the number of induced subgraphs that are trees rooted at such that all leaves have color . When transitioning, initialize . Transitions are as follows:
For every child of , we can either attach one of the induced subgraphs that are trees containing or ignore completely:
However, if , then we have to remove the case where the induced subgraph is just itself, because this violates the condition:
To extract our answer, we can iterate over every possible root of our induced subgraph.
- If , then we can directly add to our answer.
- Otherwise, we need to make sure that is not degree in any of the induced subgraphs we add. Thus, we subtract all the cases when is attached to exactly one of its children.
Thus, our answer will be
The time complexity for this approach is , because for each color, we iterate over all nodes.
Here is a (TLE) code that demonstrates this approach:
#include <bits/stdc++.h>using namespace std;using ll = long long;constexpr int MAX_N = 2e5 + 1;constexpr int MOD = 998244353;int n, a[MAX_N];ll dp[MAX_N], ans;
Virtual Tree Optimization
To accelerate our dynamic programming approach, we can observe that our dynamic programming transitions are relatively simple when involving certain types of nodes.
The most simple case of this is when a node has no nodes of color in its subtree. Here, we can simply conclude , because it is impossible to construct an induced subgraph in the subtree of with leaves of color .
Another case of simple transitions is when only one child of has any nodes of color . Then, from our previously established dp transitions, we observe that is equivalent to .
Let be the set of nodes excluding these two cases. More formally, if we let , then
We define to be the virtual tree or auxillary tree of . We can also define , the virtual parent of as the lowest node in such that and , and as a virtual child of .
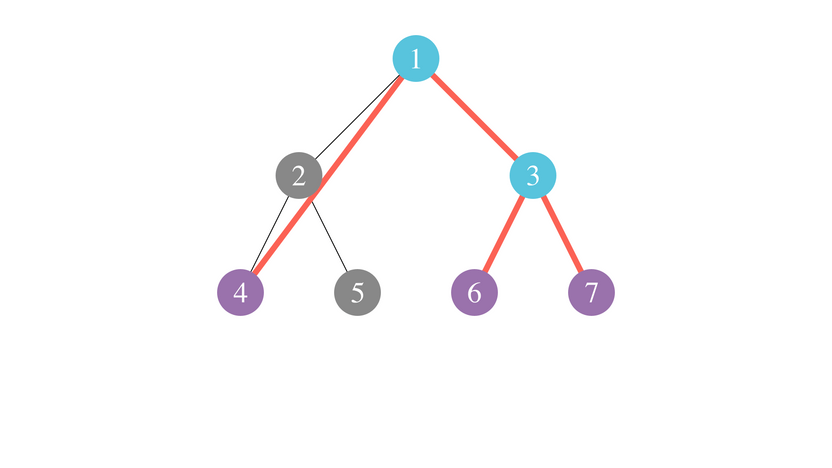
Here is an example of a virtual tree, with nodes in colored purple, and the rest of the virtual tree in blue:
From here, we can calculate our dp values similarly to before, except we only process nodes in , and we consider virtual children instead of direct children.
Notice that when calculating our answer, we also only need to consider nodes in . Nodes not in can not be the root because only one of their children have nodes of color in their subtree, meaning that we will end up with a degree node not of color .
Thus, our time complexity will be , since we iterate over the set for each distinct color.
In the following section, we prove that is bounded by , and also demonstrate how to construct a virtual tree.
Virtual Tree Construction
A well-known method to construct the virtual tree of set is as follows:
- Sort the points in by DFS order, and add them to
- Calculate the LCA of any two adjacent key points in , and add that to
- Build the virtual tree based on the ancestor-descendant relationship of the original tree
For a rough proof of correctness, consider the following:
Observe that a vertex must either satisfy or there exist at least two distinct children of with key points in their subtrees.
The former is taken care of immediately in step 1. In the latter case, as a property of DFS order, there must exist key points in the subtree of such that are in distinct subtrees and are adjacent in the DFS order when only considering key points. Because is , our construction necessarily holds true. A corollary of our construction is that is indeed bounded by - in fact, a tight bound is .
Implementation
Below is an implementation for the task, which also contains general code for constructing virtual trees. Because is , and we sort by DFS order, our final time complexity is .
#include <bits/stdc++.h>using namespace std;using ll = long long;constexpr int MAX_N = 2e5 + 1;constexpr int LG = 18;constexpr int MOD = 998244353;int n, a[MAX_N];
Problems
Warning!
Note that Bridges: The Final Battle requires concepts from Offline Deletion and BCCs and 2CCs to solve.
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| Gym | Normal | Show TagsVirtual Tree | ||||
| CF | Hard | Show TagsVirtual Tree | ||||
| CF | Hard | Show TagsVirtual Tree | ||||
| Gym | Insane | Show TagsBlock Cut Tree, Virtual Tree | ||||
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!