Table of Contents
IntroductionRestaurant CustomersSolutionImplementationClosest PairSolution 1ImplementationSolution 2ImplementationLine SegmentsSolution - Cow Steeplechase IIImplementationProblemsManhattan MSTSolution - Grid MSTImplementationProblemsRadial SweepSolution - Seeing the BoundaryImplementationProblemsIntroduction
Imagine you have a vertical line that "sweeps" the plane from left to right. That's the main idea behind the sweep line.
You might be thinking "wait - isn't keeping track of the sweep line at all possible positions super inefficient?" And you'd be correct. However, we don't actually need to keep track of the sweep line at all possible positions - only at the "critical" positions (e.g. points and intersections).
This section is not complete.
should the reader already be familiar with the 1D case (union of intervals on number line?) never explicitly mentioned in the module
| Resources | |||||
|---|---|---|---|---|---|
| CPH | |||||
| TC | |||||
Restaurant Customers
Focus Problem – try your best to solve this problem before continuing!
View Internal SolutionSolution
The solution uses a sweep line approach. Each interval is converted into two events: for an arrival and for a departure. This produces events in total.
All events are sorted by time; if two events coincide, departures are processed before arrivals. Traversing the sorted list from left to right, we maintain a counter of active customers. The counter is incremented on arrival events and decremented on departure events. The maximum value reached during this traversal is the answer.
For example, intervals yield the event sequence with counters . The maximum is .
Creating events takes , sorting them takes , and the sweep is . Thus, the overall complexity is .
Implementation
Time Complexity:
C++
#include <bits/stdc++.h>using namespace std;int main() {int n;cin >> n;vector<pair<int, int>> events;for (int i = 0; i < n; i++) {int arrival, departure;
Closest Pair
Focus Problem – try your best to solve this problem before continuing!
Solution 1
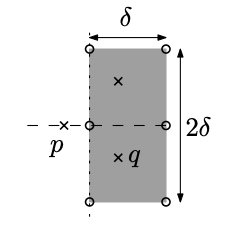
We will use a divide and conquer algorithm. First, sort the points by x-coordinate. Now, let be the subarray of points in the current step. Then, partition into two groups and representing the left and right halves of . Let and be the answer of and respectively, and define as .
Then is the upperbound of the answer. If a more optimal answer exists, it must bridge the two halves of the array (i.e. one of its endpoints is in and the other is in ). Let be the x-coordinate of any median of . Define two sets and such that and
A brute force matching algorithm that computes for all , would have a worst-case runtime of (recall that and may have up to points). However, because we are searching for distances of at most , it suffices for each to check all points .
It can be shown that for each point , there is a constant number of points that satisfy this property. Because each point in is at least apart, arranging the points in the worst case would result in 6 points in the corners and sides of the bounding rectangle.
To achieve the desired complexity per layer, we need to be able to efficiently get the points sorted by both x-coordinate (for dividing ) and y-coordinate (for matching between and ). This can be achieved by taking advantage of the merge-sort-like algorithm: sort by x-coordinate in the beginning, then for each step, merge the y-coordinates recursively.
Because each step now runs in linear time and there is a total of steps, by the master theorem our solution now runs in .
Implementation
Time Complexity:
C++
#include <bits/stdc++.h>using namespace std;struct Point {long double x, y;bool operator<(const Point &other) {if (x == other.x) { return y < other.y; }return x < other.x;}};
Solution 2
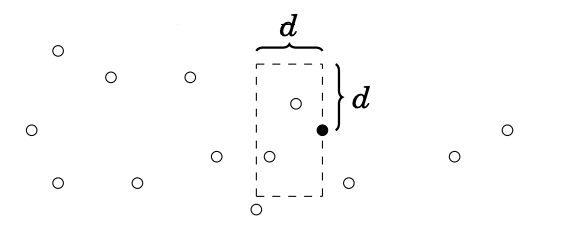
Extending Solution 1, we can use a set instead of divide and conquer. Once again, we define as the shortest distance between two points so far. After sorting the points by x-coordinate, we iterate through them while maintaining a running window containing the y-coordinates of all points in .
As we visit point , we utilize the set to consider all points with y-coordiate in . The set contains because of how it is maintained as a running window. Now we have the same bounding box as Solution 1, with at most 6 points inside.
For each point, we recalculate , and update our set accordingly. Each point is inserted and removed from the set at most once, so the algorithm yields .
Implementation
Time Complexity:
C++
#include <bits/stdc++.h>using namespace std;using ld = long double;int main() {int n;while (cin >> n && n > 0) {vector<pair<ld, ld>> points(n);for (auto &p : points) { cin >> p.first >> p.second; }
Line Segments
Focus Problem – try your best to solve this problem before continuing!
Solution - Cow Steeplechase II
Let's simplify the problem a little bit and focus on finding any overlapping segments.
To find a pair of overlapping segments, use a sweep line approach by sweeping a vertical line across the scene from left to right, pausing at every segment endpoint.
We simulate this by sorting all the segment endpoints by and walking through the sorted array (called 'events' in the code below). As we scan, we keep track of active segments using a set (called 'active_segments' in the code below). When we hit the beginning point of a segment, add it to the active set, and remove it from the active set when we hit the ending point of a segment.
Inserting or removing the active segments from the set takes per operation.
The active set of segments is ordered by coordinate. If two segments overlap, they are adjacent in the set, so every time we insert or remove a segment, we check if the adjacent segments overlap.
Here is an animation of how it works:
Implementation
Time complexity: .
C++
#include <bits/stdc++.h>using namespace std;long long sweep_line_x;Code Snippet: Point Structure (Click to expand)Code Snippet: Segment Structure (Click to expand)int sign(long long x) {
Problems
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| Old Silver | Easy | Show TagsSweep Line | ||||
| Old Gold | Normal | Show TagsSweep Line | ||||
| COI | Hard | Show TagsSweep Line | ||||
| CEOI | Hard | Show TagsSweep Line | ||||
| CEOI | Very Hard | Show TagsSweep Line | ||||
| Baltic OI | Very Hard | Show TagsSweep Line | ||||
Manhattan MST
Focus Problem – try your best to solve this problem before continuing!
Solution - Grid MST
The key observation is that although there are many points, they're spread across a pretty small surface. Because of this, instead of using Kruskal's or Prim's algorithm, we can use Dijkstra's. Starting from an arbitrary point, we run Dijkstra's algorithm with a priority queue that will sort the points by their distance to the MST.
Implementation
Time Complexity: , where is the grid size
C++
#include <bits/stdc++.h>using namespace std;const int GRID_SZ = 1000;const int dx[4] = {-1, 0, 1, 0};const int dy[4] = {0, 1, 0, -1};int main() {int n;cin >> n;
Problems
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| CSA | Hard | Show TagsManhattan MST | ||||
Radial Sweep
Instead of a vertical line sweeping the plane from left to right, radial sweep involves a ray that rotates around a central point (like a radar screen):
In this case, we sort points/events by their bearing instead of by their x- and y-coordinates. Besides that, the mechanics are the same as those of normal line sweep.
Focus Problem – try your best to solve this problem before continuing!
Solution - Seeing the Boundary
In this problem, there are three types of events: when our ray hits a fence post, enters a rock, or exits a rock.
The second and third types of events can be found for each rock by sorting the rays to its vertices by bearing and then taking the two endpoints of the sorted list. These two rays are the two tangents to the rock.
We can then perform a radial sweep to find the fence posts that Farmer Don can see - these fence posts are simply the ones where the number of type-2 and type-3 events we've processed so far are equal.
Note that some optimizations (e.g. not constructing the list of fence posts explicitly) may be required to get 100 points.
Implementation
Time Complexity:
C++
#include <bits/stdc++.h>#define x first#define y secondtypedef long long ll;using namespace std;const double PI = 4 * atan(1);struct Event {short type, id;
Problems
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| CEOI | Easy | Show TagsBinary Search, Radial Sweep | ||||
| POI | Normal | Show TagsRadial Sweep | ||||
| APIO | Hard | Show TagsRadial Sweep | ||||
| JOI | Very Hard | Show TagsRadial Sweep | ||||
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!