Baltic OI 2017 - Toll

Official Analysis

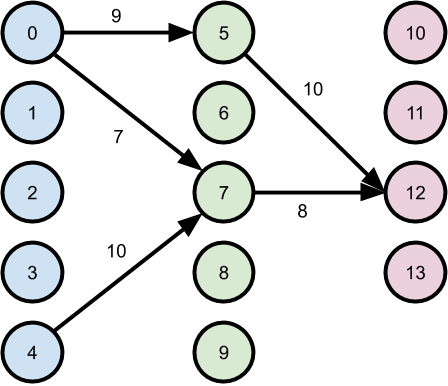
Solution

Split the graph into $N / K$ "layers" with $K$ nodes each. Notice how this graph somewhat resembles a neural network.

Let $dp[a][b][x][y]$ denote the minimum cost of a path between nodes $Ka + x$ to $Kb + y$.

For any triple $a < b < c$, the following recurrence holds:

This is known as the $(\min,+)$ product.

To finish, we can use any algorithm that allows us to quickly answer static range queries (ex. divide & conquer). Another approach is to use a sparse table. Instead of storing each DP state, we can store only $dp[i][i + 2^j][x][y]$ for each $i$, $j$, $x$, and $y$. Then we can find the value of $dp[\lfloor A / K \rfloor][\lfloor B / K \rfloor][A \% K][B \% K]$ in $\mathcal{O}(K^2 \log N)$ time per query with binary jumping. This gives a time complexity of $\mathcal{O}(K^2(N+O)\log N)$.

Implementation

$\mathcal{O}(K^3 \log N)$ per query. We can reduce this to $\mathcal{O}(K^2 \log N)$ per query by only storing the a % k-th row of ans.

Copy
#include <bits/stdc++.h>
using namespace std;

int k, n, m, o;
int dp[50000][17][5][5], ans[5][5], tmp[5][5];

void combine(int target[5][5], int a[5][5], int b[5][5]) {
	for (int x = 0; x < k; x++) {
		for (int y = 0; y < k; y++) {
			for (int z = 0; z < k; z++) {

Copy
MAX_K = 5
MAX_J = 17


def combine(target: list[list[int]], a: list[list[int]], b: list[list[int]]):
	for x in range(k):
		for y in range(k):
			for z in range(k):
				target[x][y] = min(target[x][y], a[x][z] + b[z][y])