LC - Maximum Number of Darts Inside of a Circular Dartboard

Explanation

The general idea is the following: we can try finding the answer by placing the circle's boundary on each point, then sweep - or rotate - the circle around the point to see the maximum number of points that can be inside the circle. The picture below depicts how the sweep works:

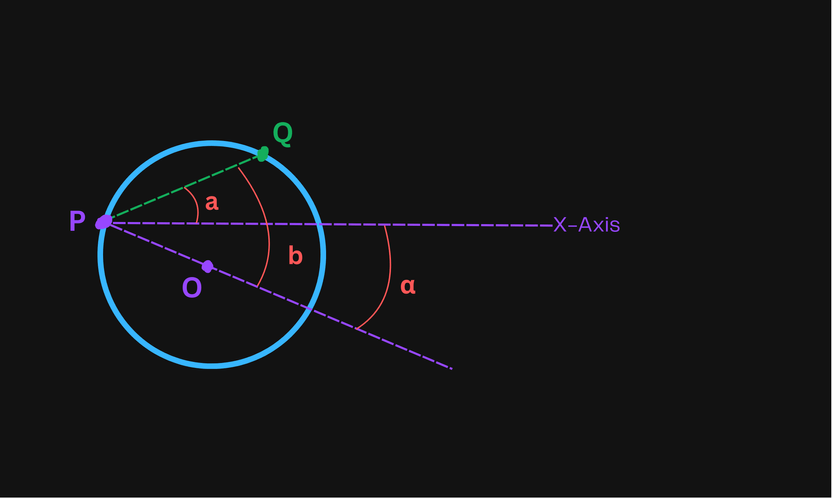
The sweeping around point $p$ can be done in $\mathcal{O}(N \cdot \log{N})$ by computing for each point the angle of entering and exiting the circle. Afterward traverse the sorted array of angles while keeping track of active points i.e. points lying inside the circle. The considered angles will be relative to the center of the circle. Let's analyze how to find the entrace angle for a point:

We'll express the values of the angles in radians. The angle of entering the circle in this case is $\alpha$ which can be expressed as: $\alpha = b - a$. Angle $a$ is right above the x-axis so it's just $\arctg$. Consider that $b=\angle{QPO}$ is an angle in the right triangle $\triangle QPL$, where $L$ is the dimetral opposite point of $P$ on the circle, therefore $\angle{PQL}=90\degree$. In this case, knowing that $PL=2 \cdot r$ - diameter - and $PQ=\texttt{dist}(P,Q)$, the angle $B$ can be conveniently expressed as $\arccos$. Consequently, the angles $a, b$ have the following formulas:

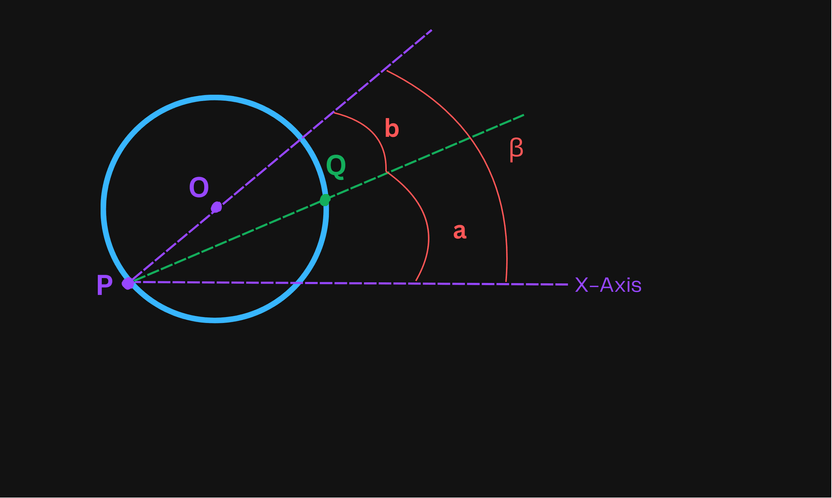
Now that we know how to find the entrance angle, it'll be easier to find the exit angle. With the same notations as the previous one - $a, b$ having the same formulas - consider this:

It can be observed that: $\beta = a + b$.

This algorithm is known as angular sweep or disk partial covering problem.

Implementation

Time Complexity: $\mathcal{O}(N^2 \cdot \log{N})$

Copy
class Solution {
  public:
	int numPoints(vector<vector<int>> &darts, int r) {
		vector<vector<double>> dist(darts.size(), vector<double>(darts.size()));
		// Compute the distance between points
		for (int i = 0; i < darts.size(); i++) {
			for (int j = i + 1; j < darts.size(); j++) {
				int dx = darts[i][0] - darts[j][0];
				int dy = darts[i][1] - darts[j][1];
				dist[i][j] = dist[j][i] = sqrt(dx * dx + dy * dy);

Copy
class Solution:
	def numPoints(self, darts: List[List[int]], r: int) -> int:
		# Compute the distances between all pairs of points
		dist = [[0] * len(darts) for _ in range(len(darts))]
		for i in range(len(darts)):
			for j in range(i + 1, len(darts)):
				dx = darts[i][0] - darts[j][0]
				dy = darts[i][1] - darts[j][1]
				dist[i][j] = dist[j][i] = math.sqrt(dx * dx + dy * dy)