CSES - Planets Queries II

In this problem, we are given a functional graph and asked $q$ queries for the minimum distance between two vertices $u$ and $v$.

Structure of the Graph

Notice that all functional graphs can be broken down into a bunch of "components". Each of these components consists of many trees directed towards the root, and a single cycle composed of said roots and some other nodes.

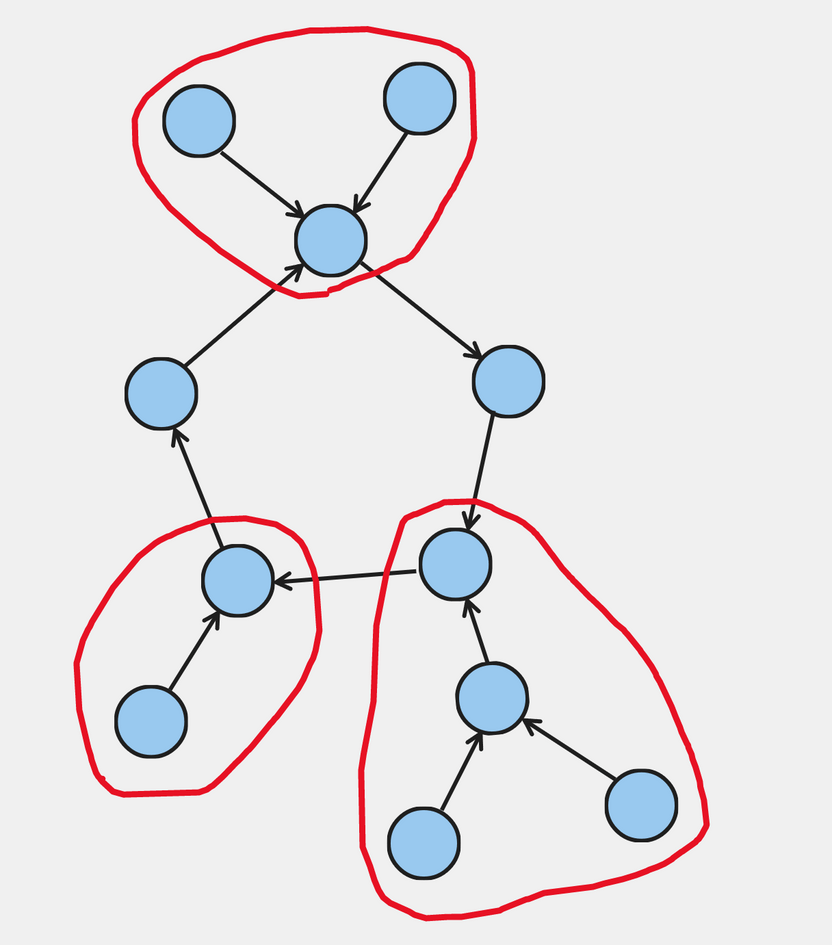
Here's an example of a possible "component". The trees are circled in red:

Given this, we can essentially break down each query into three cases:

Both in Tree

If both $u$ and $v$ are in a tree, we first have to get the distance from each node to the cycle. This can be precalculated for all nodes with BFS.

First of all, if $v$'s distance is greater than that of $u$'s, we can't get to $v$ because using a teleporter can only decrease our distance to the cycle.

But if this condition isn't satsified, we start at $u$ and use the teleporters until our distance to the cycle is equal to that of $v$'s. If we've actually ended up at $v$, then our answer is the difference between the distances. Otherwise, it's impossible to reach $v$.

To see which planet we end up at if we teleport $t$ times, we can use binary jumping.

Both in Cycle

If both are in a cycle, we get both $u$ and $v$'s index in the cycle. Let's call these indices $u_i$ and $v_i$ respectively. Now, if $u_i \leq v_i$, then our answer is $v_i - u_i$. On the other hand, if $u_i > v_i$, then our answer is $\texttt{cycle\_len} - (u_i - v_i)$.

One in Each

This case is really two cases, but we only really need to consider one of them.

If $u$ is in a cycle but $v$ is in a tree, it's impossible to reach $v$ from $u$ because we can only go from a tree to a cycle, not vice versa.

On the other hand, if $u$ is the one in the tree, we get which node in the cycle $u$'s tree connects to, which is also the root. Then this reduces to a version of the second case: we just have to add the distance from $u$ to the root as well.

Implementation

Time Complexity: $\mathcal{O}((n+q)\log n)$

Copy
#include <cmath>
#include <iostream>
#include <map>
#include <vector>

using std::cout;
using std::endl;
using std::vector;

int main() {

Copy
import java.io.*;
import java.util.StringTokenizer;

public class PlanetQueries2 {
	private static int MAX_HEIGHT = 20;
	private static int[][] binaryLifting;
	private static int[] arr;
	private static int[] len;
	private static boolean[] visited;