Introduction
Graphs can be used to represent many things, from images to wireless signals, but one of the simplest analogies is to a map. Consider a map with several cities and bidirectional roads connecting the cities. Some problems relating to graphs are:
Is city connected to city ? Consider a region to be a group of cities such that each city in the group can reach any other city in said group, but no other cities. How many regions are in this map, and which cities are in which region? (USACO Silver)
What's the shortest distance I have to travel to get from city to city ? (USACO Gold)
For USACO Bronze, it suffices to learn the basics of how graphs are represented (usually adjacency lists).
| Resources | |||||
|---|---|---|---|---|---|
| CSA | interactive | ||||
| CSA | interactive - adjacency lists and matrices | ||||
| CSA | use this tool to visualize your own graphs | ||||
| CPH | graph terminology, representation | ||||
| IUSACO | graph basics and representation, trees | ||||
| PAPS | adjacency matrices, lists, maps | ||||
Constructing Adjacency Lists
Graphs are often given as input in the following format:
- The first line will contain the number of nodes and the number of edges .
- Then follow lines, each containing a pair of integers specifying an edge of the graph.
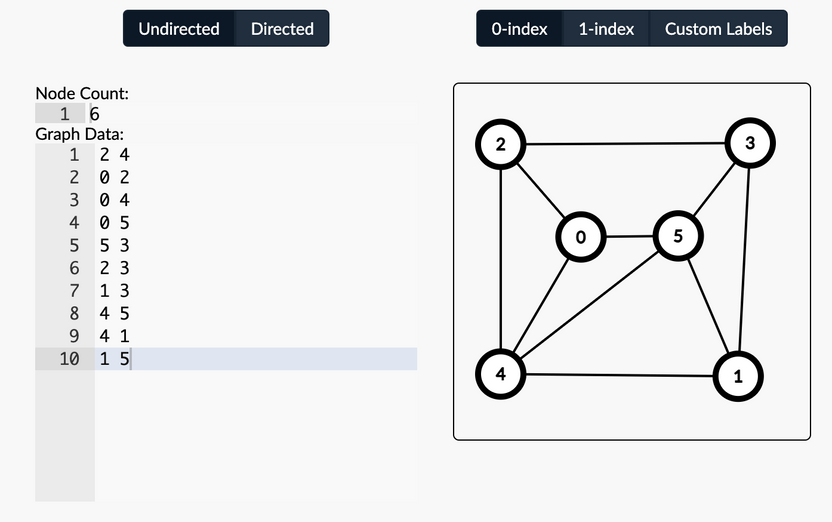
For example, the undirected graph given in the CSAcademy resource from above would be represented as the following input:
6 10 2 4 0 2 0 4 0 5 5 3 2 3 1 3 4 5 4 1 1 5
and could be visualized in the CSAcademy graph editor:
The following code represents the graph using adjacency lists. Once we have the graph in this representation, it is easy to print the number of neighbors of a node, or iterate over the neighbors of a node.
C++
#include <iostream>#include <vector>using namespace std;int main() {int N, M;cin >> N >> M;vector<vector<int>> adj(N);for (int i = 0; i < M; ++i) {int u, v;
Java
import java.io.*;import java.util.*;public class Main {public static void main(String[] args) throws IOException {BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));StringTokenizer s1 = new StringTokenizer(reader.readLine());int N = Integer.parseInt(s1.nextToken());int M = Integer.parseInt(s1.nextToken());
Python
N, M = map(int, input().split())adj = [[] for _ in range(N)]for i in range(M):u, v = map(int, input().split())adj[u].append(v)adj[v].append(u)u = 1# print number of vertices adjacent to uprint("deg(u) =", len(adj[u]))# print all edges with u as an endpointfor v in adj[u]:print("{" + str(u) + ", " + str(v) + "}")
Output:
deg(u) = 3
{1, 3}
{1, 4}
{1, 5}What Does a Bronze Graph Problem Look Like?
All of the problems below fall into at least one of the following two categories:
- The graph's structure is special (it's a tree, path, or a cycle).
- To solve the problem, all you need to do is iterate over the adjacency list of every vertex.
In addition, knowledge of Silver-level graph topics is usually helpful but not strictly required to solve the problem.
Livestock Lineup
Focus Problem – try your best to solve this problem before continuing!
View Internal SolutionWhile the intended solution is to brute force all possible permutations of the cows in time, we can solve the problem in just time if we represent the constraints using a graph.
Solution Using Graphs
Warning!
This explanation, and the implementation that follows, assume that all constraints in the input describe distinct pairs of cows. If this assumption did not hold, you would first need to remove duplicate constraints.
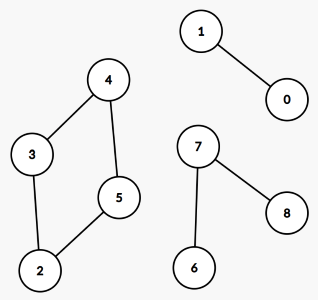
Notice that since the input is guaranteed to be valid, we're always going to end up with "chains" of cows that we can arrange as we please. Using the sample given in the problem, we'd get a "chain" representation like this:
Note that cows that are not part of any chain can be considered their own chains of length 1 for implementation purposes.
With this representation in mind, we can iterate through the cows in lexicographical (alphabetical) order. When we visit a cow that could be a possible start of a chain (a cow that has at most one required neighbor), we repeatedly go through its neighbors, adding the cows we visit to the ordering, until we hit an end.
Implementation
Time Complexity:
C++
#include <algorithm>#include <fstream>#include <map>#include <string>#include <vector>using std::endl;using std::string;using std::vector;
Java
import java.io.*;import java.util.*;public class LineUp {// Assumed to be in sorted order (which it is)static final String[] COWS = new String[] {"Beatrice", "Belinda", "Bella", "Bessie", "Betsy", "Blue", "Buttercup", "Sue"};public static void main(String[] args) throws IOException {Map<String, Integer> cowInds = new HashMap<>();
Python
COWS = sorted(["Bessie", "Buttercup", "Belinda", "Beatrice", "Bella", "Blue", "Betsy", "Sue"])cow_inds = {c: i for i, c in enumerate(COWS)}neighbors = [[] for _ in range(len(COWS))]with open("lineup.in") as read:for _ in range(int(read.readline())):words = read.readline().strip().split()
Check Your Understanding
Problems
| Status | Source | Problem Name | Difficulty | Tags | ||
|---|---|---|---|---|---|---|
| Bronze | Hard | Show TagsColoring | ||||
| Bronze | Hard | Show TagsDFS, Tree | ||||
| Bronze | Hard | Show TagsFunctional Graph | ||||
| Bronze | Hard | Show TagsCycle, Permutation | ||||
| Bronze | Very Hard | Show TagsTree | ||||
| Bronze | Very Hard | Show TagsTree | ||||
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!