Official Analysis (C++ and Java)
Explanation
Although the problem may be daunting at first, it helps to think about how a smaller range is connected to another.
If equals the number of unordered triplets which sum to zero between , then what states does this rely on?
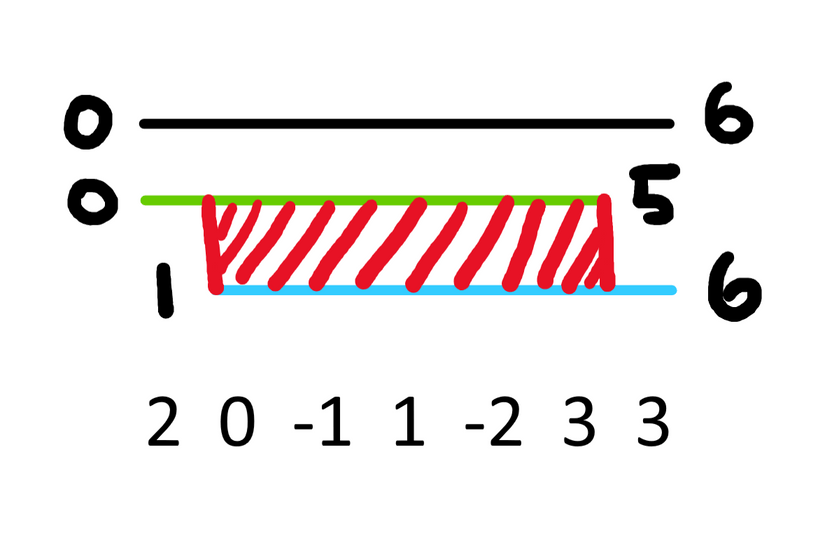
We can choose to exclude one endpoint or the other, which gives us a picture like this (reminder to make sure not to double count the overlap).
While this'll count all the triplets in between them, we aren't taking into account any triplets which use both the elements at and , since those aren't included in our "PIE-like" transition.
To do this, we can precalculate the number of triplets which start at and end at in time by storing the occurrences of the compliment of and in an array.
More formally, our final transition is:
where equals the number of triplets which sum to zero and start at and end at .
Implementation
Time Complexity:
Note that we can't store in its own array due to memory constraints.
C++
#include <bits/stdc++.h>using namespace std;using ll = long long;const int MAX_VAL = 1e6;int main() {freopen("threesum.in", "r", stdin);freopen("threesum.out", "w", stdout);cin.tie(0)->sync_with_stdio(0);
Java
import java.io.*;import java.util.*;public class Threesum {static final int MAX_VAL = 1000000;public static void main(String[] args) throws IOException {Kattio io = new Kattio("threesum");int N = io.nextInt();int Q = io.nextInt();int[] a = new int[N];for (int i = 0; i < N; i++) { a[i] = io.nextInt(); }
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!