AC - Xor Pyramid

Explanation

Simulating the process, similarly to Pascal's triangle, isn't efficient, because of $n$ being too large. One good practice when dealing with such problems is analyzing how the answer is affected by each single value. Keeping in mind that xor is its own inverse, a value $x$ xored with itself an even number of times will result in $0$, thus canceling each other out; on the other hand, the value $x$ xored with itself and odd number of times will simply result in $x$. Consequently, we can shift our focus to finding for each bottom value the number of times it will affect in the top value.

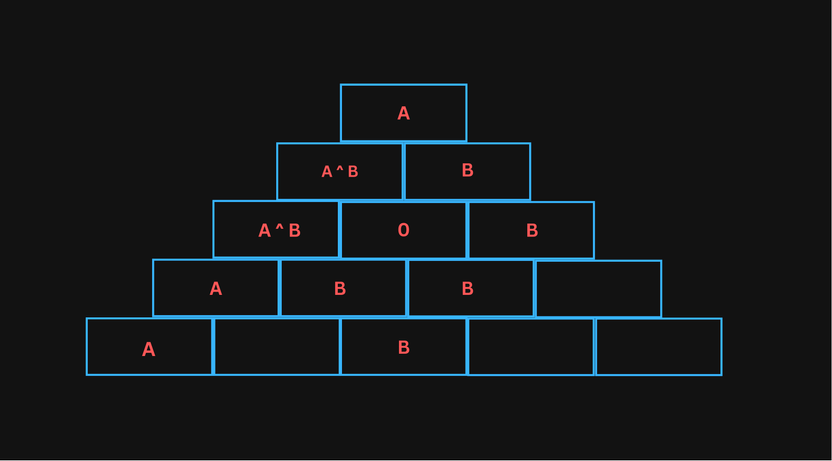
Let's take a look at how bottom values modify the final result.

As you can see, the value $B$ does not appear in the final result, thus it can be ignored. Additionally, the bottom row values in Pascal's triangle of height five are $1,4,6,4,1$. We can think of these values as the number of occurrences of each bottom row value. In the above image, value $A$ will be xored one time in the result, while value $B$ will be xored four times in the result. Therefore, the parity of the frequency tells us that value $A$ contributes to the result, while value $B$ cancels out itself.

Because we are only interested in the parity of the binomial coefficient, there is no need to compute its actual value. We can simply check the parity by counting the power of two in $\binom{n}{k}=\frac{n!}{k! \cdot (n-k)!}$. With this in mind, precompute $\texttt{pref}_i=p$ where $p$ is the power of two in $i!$ factorization. Therefore, the binomial coefficient is odd if: $\texttt{pref}_n-\texttt{pref}_k-\texttt{pref}_{n-k}=0$.

Implementation

Time Complexity: $\mathcal{O}(N)$

Copy
#include <iostream>
#include <vector>

using namespace std;

int main() {
	int n;
	cin >> n;
	vector<int> pref(n + 1);
	for (int i = 2; i <= n; i++) {

Copy
import java.io.*;
import java.util.*;

public class XorPyramid {
	public static void main(String[] args) throws IOException {
		BufferedReader f = new BufferedReader(new InputStreamReader(System.in));
		PrintWriter out = new PrintWriter(System.out);
		StringTokenizer st = new StringTokenizer(f.readLine());

		int n = Integer.parseInt(st.nextToken());

Copy
n = int(input().strip())

# Initialize prefix array
pref = [0] * (n + 1)

# Calculate the number of trailing zeros in each number up to n
for i in range(2, n + 1):
	num = i
	while num % 2 == 0:
		pref[i] += 1