COCI 2016 - Burza

Official Analysis

Explanation

Initial Analysis

Let's first try to transform the terms of the game into something less arbitrary.

Since Stjepan can't backtrack because he marks all nodes he visits himself, he can only move down the tree, increasing his depth as he goes. Given this, we can make a series of observations:

1. Daniel can effectively "cut off" an entire subtree by marking a node, because then Stjepan can't get through that one node. Note that this node has to be at a level deeper than Stjepan's current level.
2. If we can't prevent Stjepan from reaching a node of depth $k$ (with the root being of depth $0$), then the game cannot always end in at most $k$ moves.
3. Since we've already "lost" if Stjepan reaches depth $k$, we don't care about anything below depth $k$. We can also remove any nodes that don't lead to a depth of at least $k$. Note that we won't consider any of these irrelevant nodes from here.

From the first observation, we can see that an optimal strategy would be to mark at most one node at each depth (excluding the root).

Since marking a node of depth $d$ makes at least $k - d + 1$ nodes off-limit and we can mark nodes from depth $1$ to $k$, if $\frac{k \cdot (k + 1)}{2} \geq n$, the game can always end in $k$ moves.

That reduces the maximum value of $k$ we have to consider down to around 30, which unfortunately is still too large for an exponential time solution. But it is something! Let's see if we can cut the bounds down further: 20 would be a good breakpoint.

Further Analysis

To limit the maximum number of steps to a point where bitwise DP is feasible, we have to prove that a game can always end in $k$ moves if $k^2 \geq n$.

Since each move results in breaking a tree down into a bunch of smaller trees, we can do a proof by induction.

Let's define $n_r$ as the total number of nodes that haven't been made invalid yet after $r$ moves, and $t_r$ as the number of valid nodes Stjepan can move to after $r$ moves (aka the number of valid nodes of depth $r+1$).

For example, let's say that we were at a depth of 1 in the following tree:

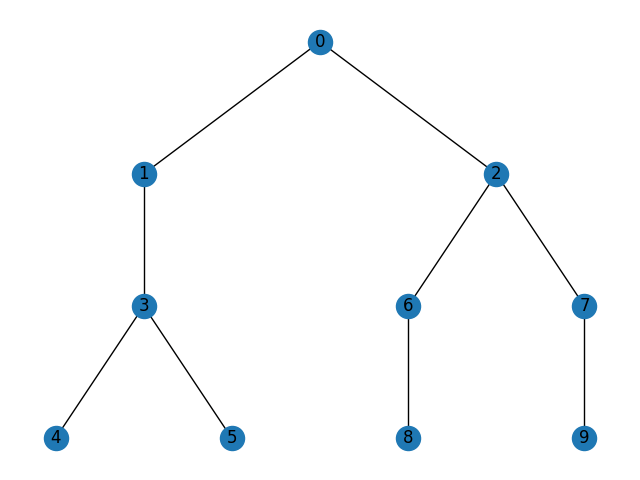
If we cut off node 2, $n_1$ would be 3 and $t_1$ would be 1, since Stjepan can only move to node 3.

Our base case for the induction is the following:

This is true for $r=0$. Now, we just have to show that given the above,

If we show this, we'll know that $n_r \leq (k-r)^2$ for all $r$. Setting $r=k$, we get $n_k \leq (k-k)^2=0$, which effectively means that it's possible for us to make all nodes invalid after $k$ moves.

To prove this, let's first define a more concrete strategy:

At each level, cut off the node with the largest subtree size that hasn't been already cut off. If there's multiple nodes with this quality, cut off any of them.

If we follow the strategy defined earlier, at each turn we'll always cut off at least $\frac{n_r}{t_r}$ nodes and also leave $t_r - 1$ nodes behind, since they're now above our current depth*. This yield the following inequality:

While this is a meaningful relationship, the $t_r$ terms are a bit nasty. It'd be great if we could just have a relation between $n_r$ and $n_{r+1}$.

Fortunately, through algebraic manipulation, it is possible to obtain the following inequality:

Chaining this with the above inequality, we get

Since we know that $n_r \leq (k-r)^2$ and by extension $\sqrt{n_r} \leq k-r$, we can substitute those terms to prove our desired expression:

And we're done! Since we've shown that any case where $k^2 \geq n$ will result in a win, we just have to handle the case where $k \lt 20$, for which bitmask DP will suffice.

Bitmask DP

Note that since a tree is a planar graph, any node we cut off will cover a continuous segment of leaves.

Take the following tree as an example:

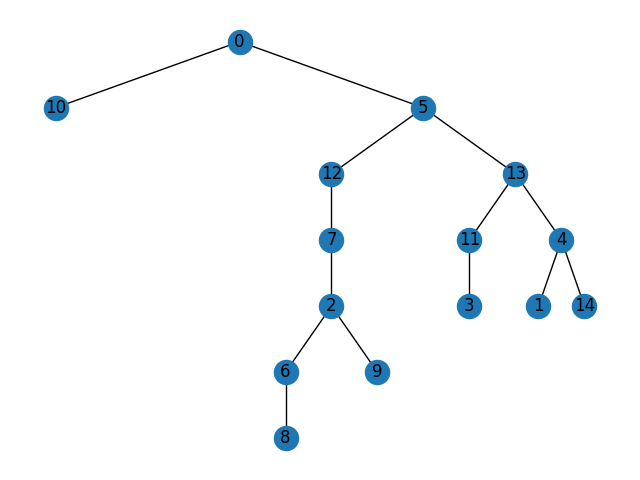
No node can cover only, say, 3 and 14. If it can cover those two then it also must cover node 1.

This leads us to our DP state. Let $\texttt{max\_cover}[S]$ be the maximum number of leaves we can cover from the start given we take one node from each depth specified in the subset.

For our transition, we try adding on depths to all previous subsets and iterate through all nodes in those depths.

For example, if removing a node could cover the third leaf to the fifth leaf and our current previous subset can cover up to the fourth leaf, then putting those two together yields a configuration that can cover up to the fifth leaf.

Implementation

Time Complexity: $\mathcal{O}(2^{\sqrt{n}} \cdot n)$

Copy
#include <functional>
#include <iostream>
#include <map>
#include <vector>

using std::cout;
using std::endl;
using std::vector;

int main() {