CF - Tree Painting

Official Editorial

Explanation

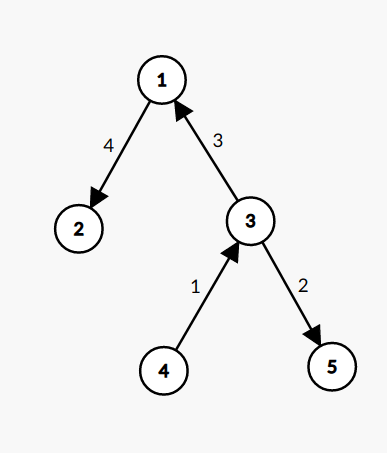
Notice that choosing a leaf node is more optimal than choosing anything in the middle because that way we have the entire size of the rest of the tree as a part of the leftover connected component. This hints for a DP on Trees solution, where we choose one leaf node, work our way up through that leaf node's ancestors and work our way down for each of our ancestor's siblings, incorporating the maximum possible cost for each of their subtrees. For example, for the following tree:

If we select the 4th node as our starting point, then the process would look like the following:

1. Work our way up to 3
2. Work our way down to 5
3. Work our way up to 1
4. Work our way down to 2

We need to maintain the cost of two different scenarios for each node: working up from a leaf node to the current node and working down from the current node throughout its whole subtree, meaning that we have to maintain 2 DP arrays. Let's define the DP transitions for each of the arrays. We will use $dp_1$ for the cost of working down and $dp_2$ for the cost of working up and $sz$ for the size of a subtree.

We can calculate this DP array with a single DFS search. Now, for the second DP array:

There is still one problem though. The cost of $sz[u] - sz[c]$ is multiplied by the number of nodes between the current node and the initial node inclusive. However, we can't anticipate this number beforehand, and we might have some ancestor node later on which would have prefered a higher distance over a higher cost. This means that we need to incorporate the $sz[u] - sz[c]$ for every ancestor node when initializing the $dp_2$ value for leaf nodes. That way we, it will be incorporated into the cost beforehand and we don't need to worry about choosing the wrong initial node with an inoptimal ending cost.

We can calculate these initial values with another DFS search before the one calculating the values for $dp_2$. That way we can remove the term including $sz[u] - sz[c]$ from the recurrence formula for $dp_2$. To calculate these initial values, we notice that every time we go down by one depth, we add size of all the siblings and parent combined two times, one for the parent, and once for the current node. We also add the cost of all the ancestor's siblings and parent combined once more. Let's say $p_2[u]$ is the initial cost for a leaf node $u$, and $p_1[u]$ is the cost of the ancestor's siblings and parent combined till $u$. Then we can calculate $p_1[u]$ and $p_2[u]$ using the following recurrence:

Implementation

Time Complexity: $\mathcal{O}(N)$

Copy
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

vector<vector<int>> g;
vector<ll> dp1, dp2;
vector<ll> p1, p2;
vector<ll> sz;

// Calculate sz and dp1