USACO Silver 2019 February - The Great Revegetation

Official Analysis (C++)

Explanation

Assume that we have a valid solution composed of $K$ connected components in our graph.

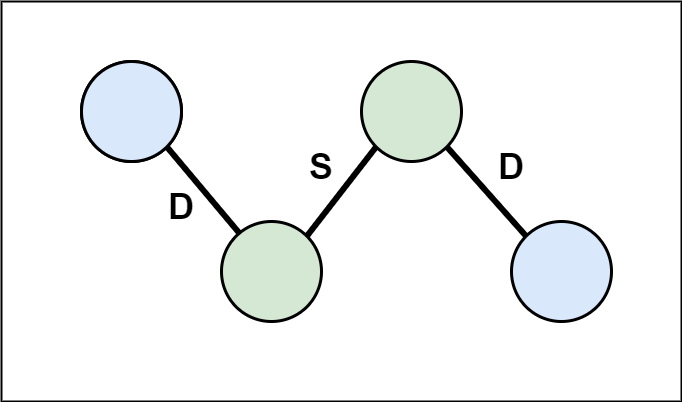
Let's look at one of these connected components, which could look something like this:

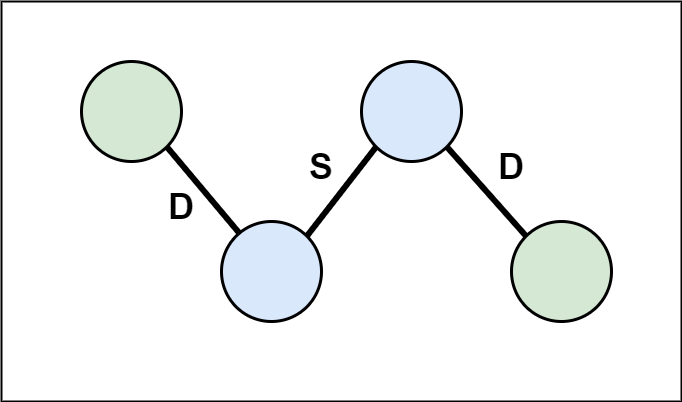
However, for each of the $K$ connected components, the grass types can be inverted and still be a valid solution:

There are $2$ possible ways to arrange each connected component. Thus, if there's $k$ connected components, there's $2^k$ ways to arrange the entire graph.

Note how the nodes force their adjacent ones to have a specific coloring, so if any two nodes don't satisfy this condition, it's impossible. Otherwise, the solution will always be $2^k$.

Implementation

Copy
#include <bits/stdc++.h>
using namespace std;

int main() {
	freopen("revegetate.in", "r", stdin);
	freopen("revegetate.out", "w", stdout);

	int n, m;
	cin >> n >> m;

Copy
import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class Revegetate {
	public static int[] type;
	public static boolean impossible;
	public static ArrayList<Integer>[] same;
	public static ArrayList<Integer>[] diff;