Official Analysis (C++)

Explanation

First, note that if $K$ is not a divisor of the $N - 1$, then the edges can never be evenly partitioned. Thus, we only need to check divisors of $N - 1$.

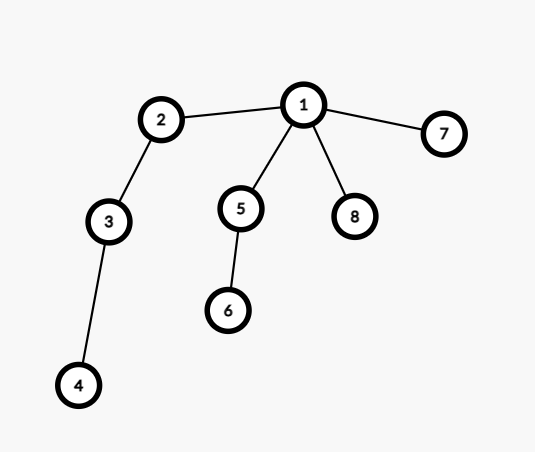
We can arbitrarily root the tree at node $1$. Let $\mathtt{toBeMerged[i]}$ store the length of the path passes through node $i$ and its length has not reached $K$ yet. Since only $1$ of such path exist, all of the other paths which source from the subtrees of $i$ must be evenly paired.

For each node $j$ such that $j$ is a child of node $i$, there must be another node $k$ such that $\mathtt{toBeMerged[j]+toBeMerged[k]} + 2 = K$ in order to complete the path. If no such $k$ exist, then we will store the current length of the path in $\mathtt{toBeMerged[i]}$, but there can only be one such $j$.

In the above tree, assume $K = 3$. Then $\mathtt{toBeMerged[2]} = 2$, $\mathtt{toBeMerged[5]} = 1$, $\mathtt{toBeMerged[7]} = 0$, and $\mathtt{toBeMerged[8]} = 0$. Since there are two paths with length $0$ and only one path with length $1$, we have a path of length $0$ left over, so $\mathtt{toBeMerged[1]} = 0 + 1 = 1$.

It can be proven the maximum number of divisors for an integer up to the constraints of $N$ will be small enough for us to run an linear time algorithm for each divisor.

Implementation

Time Complexity: $\mathcal{O}(N \cdot N^{o(1)})$

Copy
#include <bits/stdc++.h>
using namespace std;

const int N = 1e5;
vector<int> g[N];
int to_be_merged[N];

bool dfs(int node, int p, int k) {
	// count length of path not merged yet in subtrees
	map<int, int> to_be_merged_count;