Solution

The Official Editorial uses a solution with Boruvka's Algorithm. There is a simpler solution using divide and conquer.

Firstly, note that because there is essentially an edge between any pair of nodes, the values of the nodes themselves can be considered unordered. Thus, the answer will not change if we sort the elements.

Secondly, note that duplicate elements can be removed. This is because duplicate elements can be connected with an edge of 0 cost.

After these two steps, we have obtained a sorted array with no duplicates whose answer is the same as the original problem.

Now consider some subarray $[l, r]$ as well as some bit $b$ ($0 \leq l \leq r < N$, $0 \leq b < 30$). Partition the subarray into two sets $L$ and $R$, where $R$ contains all elements with bit $b$ set, and $L$ contains other elements. We will be assuming that $b$ is the first different bit; that is, all elements in the subarray have the same bits for all bits greater than $b$.

Because $b$ is the first different bit and because the array is sorted, $L$ contains some prefix of the subarray and $R$ contains some suffix. That is to say, $L = A[l:m - 1]$ and $R = [m : r]$ for some $l < m \leq r$.

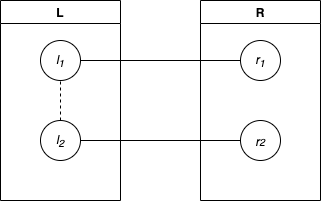
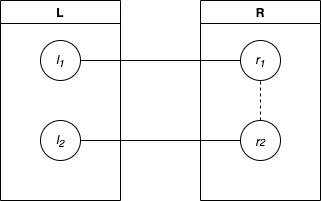
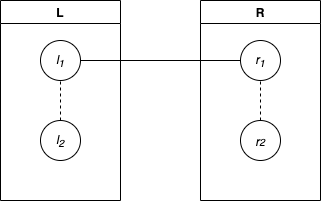
Lemma: In a minimum xor spanning tree, there is exactly 1 edge between an element in $L$ and an element in $R$.

Proof: By definition, a spanning tree must connect all vertices, which implies the existence of at least 1 edge between $L$ and $R$. Assume there is two edges between $L$ and $R$, with endpoints $(l_1, r_1)$ and $(l_2, r_2)$ respectively, where $l_1, l_2 \in L$ and $r_1, r_2 \in R$. The tree is constructed in one of the following ways, where solid lines represent edges and dashed lines represent paths.

Without loss of generality, disconnect $(l_2, r_2)$. The spanning tree becomes disconnected, with either $l_2$ or $r_2$ in the component that does not contain $l_1$ and $r_1$. It is always more optimal to connect this node to the corresponding edge node. That is, if $l_2$ is not in the same component as $l_1$, then an edge between $l_1$ and $l_2$ will always be better than one between $l_2$ and $r_2$.

By definition, $l_1$ and $l_2$ share a bit $b$, so the xor of their values does not contain bit $b$, whereas $l_2 \texttt{ xor } r_2$ always contains $b$. Note that this implies that it is always better to connect $l_2$ to $l_1$; however, this configuration may not be optimal. The proof is analogous if instead $r_2$ is disconnected. $\blacksquare$

Thus, the divide and conquer algorithm will proceed as follows: We will partition the subarray into $L$ and $R$. This step takes $\mathcal{O}(n)$ time. Note that if either $L$ or $R$ is empty (if all numbers in the range contain $b$ or if none of them contain $b$), we immediately recurse with the same subarray and $b - 1$ as the bit. Next, we will choose an element from $L$ and an element $R$ with a minimum pairwise xor, and add this to the answer. Lastly, recursively run the algorithm on $L$ and $R$ with bit $b - 1$.

How do we find two values such that their xor is minimized? One way to do this efficiently is with a trie. In the trie, each number is represented as a string of its binary representation, starting with the most significant digit and ending with the least. For xor queries, we can do a greedy traversal from root to leaf. When a transition exists that corresponds to the current bit of the query number, we greedily take that transition; otherwise, we are forced to take the unoptimal transition, and add the weight of that bit to the answer.

Implementation

Time Complexity: Let $n$ be the length of the array, and let $a$ be the value of an arbitrary element. There are $\log a \approx 30$ levels of recursion, each containing exactly $n$ elements. Furthermore, each insertion/query in the trie takes $\mathcal{O}(\log a)$ time, since we have to traverse at most the number of distinct bits in $a$. Combining this information, the total time complexity is $\mathcal{O}(n \log^2 a)$.

Copy
#include <bits/stdc++.h>
using namespace std;

const long long INF = 2000000011;

int N;
long long A[200005];

namespace Trie {
struct Node {