Official Analysis (C++)

Explanation

Let's call:

• $x_{1}$ and $x_{2}$ the leftmost and rightmost points of table 1 respectively
• $y_{1}$ and $y_{2}$ the bottommost and topmost points of table 1 respectively
• $w_{1}$ and $h_{1}$ the width and height of table 1 (equal to the difference in $x_{1}$ and $x_ {2}$ and $y_{1}$ and $y_{2}$ respectively)
• $w_{2}$ and $h_{2}$ the width and height of table 2 respectively
• $W$ and $H$ the width and height of the room respectively

The key to this problem is realising that table 2 will only ever be in 4 different positions relative to table 1: to its left, right, top or bottom (see diagram below). In addition, in all cases we can assume that table 2 will be touching its respective wall in order to (attempt) to maximise its distance from table 1. E.g., if placing table 2 to the left of table 1, we will assume its leftmost edge will be touching the left wall of the room. Determining the solution is then simply a case of simulating all of these cases and finding which involves moving table 1 the smallest distance.

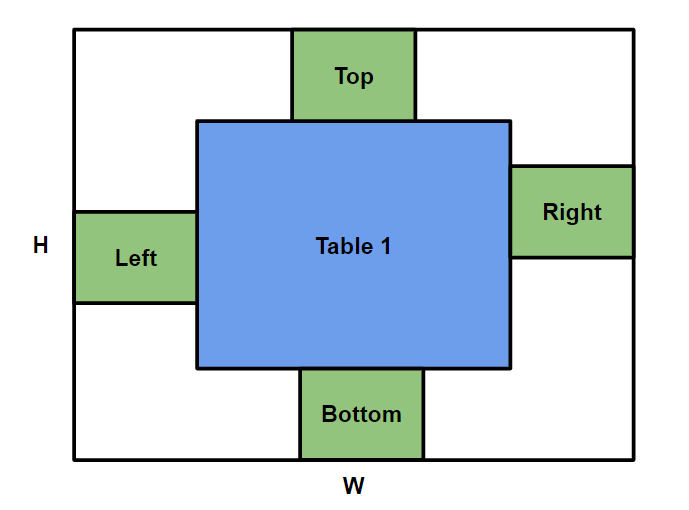Possible placements of table 2 relative to table 1.

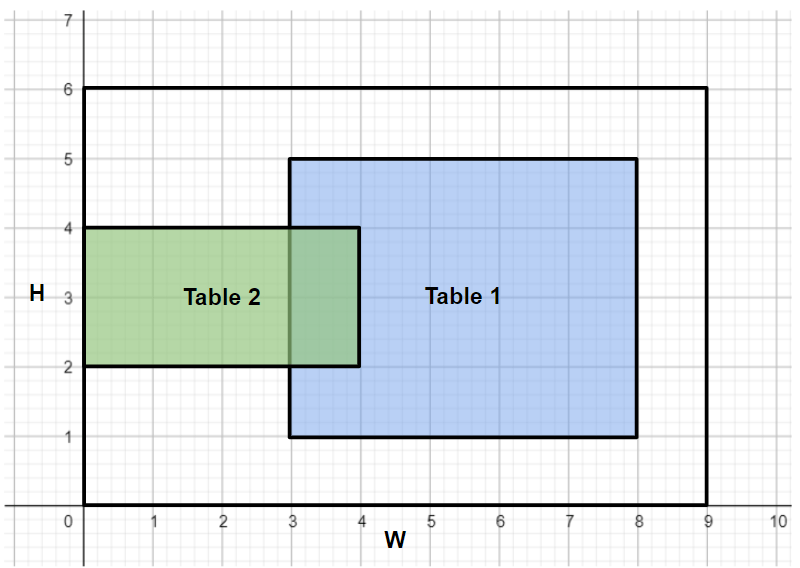
To determine the minimum distance that table 1 must be moved, we have to calculate the overlap between the two tables. For example:

In this case, table 2 is placed to the left of table 1. We can therefore calculate its overlap with table 1 as follows: $w$ - $x_{1}$. Here the overlap is 1, meaning we must move table 1 one space from its starting position to fit table 2 in the room. We must then compare this answer to the answers we get from placing table 2 to the right, top or bottom of table 1. The smallest of all of these is our final answer.

To summarise, we calculate the overlap of the two tables as follows:

• Table 2 placed to the left of table 1: Overlap = $w$ - $x_{1}$
• Table 2 placed to the right of table 1: Overlap = $x_{2}$ - ($W$ - $w$)
• Table 2 placed to the top of table 1: Overlap = $y_{2}$ - ($H$ - $h$)
• Table 2 placed to the bottom of table 1: Overlap = $h$ - $y_{1}$

It is possible that the two tables don't overlap at all. In this case the above calculations would return a negative number so we should instead return 0 to indicate that table 1 doesn't have to move at all.

Implementation

Time Complexity: $\mathcal{O}(1)$

Copy
#include <bits/stdc++.h>
using namespace std;

int main() {
	int tc;
	cin >> tc;
	for (int i = 0; i < tc; i++) {
		int total_width, total_height;
		cin >> total_width >> total_height;

Copy
for _ in range(int(input())):
	total_width, total_height = map(int, input().split())
	x1, y1, x2, y2 = map(int, input().split())
	w1 = x2 - x1
	h1 = y2 - y1
	w2, h2 = map(int, input().split())

	ans = float("inf")

	# Calculating minimum and maximum X and Y values needed to fit in their places

Copy
import java.io.*;
import java.util.*;

public class TwoTables {
	static InputReader r = new InputReader(System.in);
	static PrintWriter pw = new PrintWriter(System.out);
	public static void main(String[] args) {
		int n = r.nextInt();

		for (int i = 0; i < n; i++) {